Dans l’épisode 2 de la deuxième saison de la série Victoria, la reine éponyme rencontre Ada Lovelace et Charles Babbage. Si l’éducation de la souveraine en science l’empêche de comprendre l’intérêt de l’idée de Babbage et Lovelace, l’idée de la machine analytique est rapidement présenté. Cela nous donne l’occasion de nous pencher sur le travail de Lovelace et Babbage et son importance pour l’informatique moderne. La biographie d’Ada Lovelace est présenté dans la vidéo ci-dessus de la chaine Sur les épaules de géant·e·s. Ici nous nous concentrons sur l’idée de machine analytique de Babbage.

Machines à calculer

Très rapidement dans l’histoire humaine, l’être humain a eu besoin d’aide pour compter les grands nombres ou pour aider à retenir les décomptes. Pour cela, il a inventé les différents types de bouliers ou d’abaque. Les plus simples sont de simples décomptes d’éléments de type cailloux. Les plus utilisés sont les bouliers permettant de décomposer par unité, dizaine, centaine… qui facilite les opérations en particulier les additions et les soustractions. Mais ils nécessitent un certain nombre de manipulations comme le passage manuel entre les ordres de grandeurs (unité, dizaine…). Ce type de manipulation entraine inévitablement des risques d’erreurs.
Au XVIIe siècle, les mécanismes d’horlogerie se miniaturisent et des mathématiciens les utilisent pour automatiser ces machines à calculer. A la place des boules, il s’agit d’un cylindre qui est entrainé par des engrenages. Blaise Pascal est le premier à se pencher sur la question et invente un sautoir qui permet le report automatique des retenues. Et c’est le mathématicien Leibniz qui invente un cylindre cannelé pour permettre les multiplications. Si ce sont les prémices de la mécanisation des calculs, il faudra attendre le milieu du XIXe siècle pour que ces machines soient utilisées à grande échelle.

Les machines à différence

Mais les calculs ne s’arrêtent pas aux quatre opérations de base. Et des calculs plus complexes sont nécessaires en science, en navigation… Plus les calculs sont complexes et plus ils demandent du temps et le risque d’erreurs augmente. Pour pallier à ces soucis, on crée des règles à calculs et des tables de calculs permettant des calculs divers selon leur conception. Mais les tables peuvent contenir des erreurs et les règles dépendent de la précision des graduations. Il est également possible de simplifier certains calculs par des approximations. Cela facilite le calcul mais entraîne un manque de précision.
Dans un monde où tout se mécanise, l’idée de mécaniser la production de tables de calculs fait son chemin. Babbage a le second l’idée d’une machine à calculer des fonctions polynomiales de forme :
\[ P(x)=ax^n+bx^n-1+…+mx+z\]
Par exemple
\[ P(X)=23x^3+54x^2+36x-9 \]
L’avantage est que les fonctions polynomiales peuvent approcher des fonctions plus complexes comme les fonctions trigonométriques ou logarithmiques. Comme les multiplications et les puissances sont des calculs complexes pour une machine. Babbage utilise la technique de la méthode des différences finies. Cette méthode permet une approximation en utilisant que des additions une fois des donnes de bases liées à la fonction que l’on calculer. Cela demande néanmoins que la machine stocke des résultats intermédiaires pour les réutiliser pour la suite de ces calculs. Les résultats des calculs effectués peuvent se résumer dans un tableau :

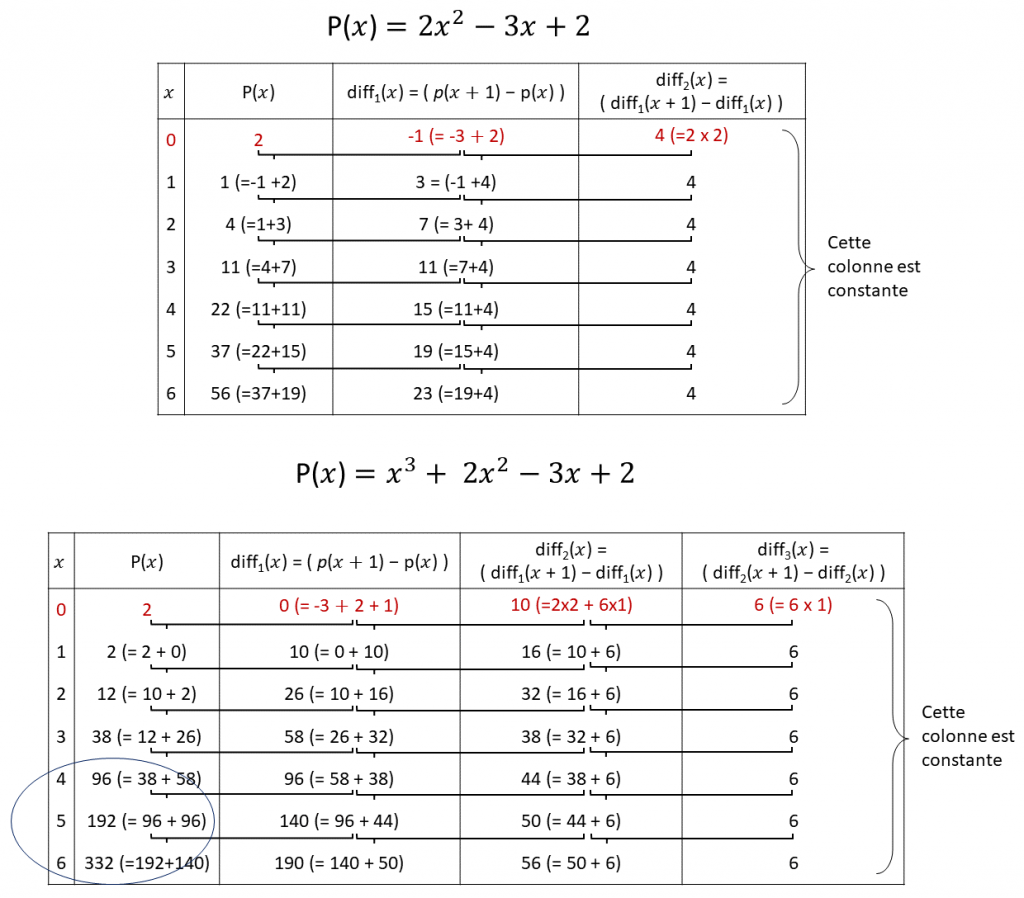
Le passage d’une ligne à une autre se fait de droite à gauche par des additions de valeur en partant du principe que la colonne la plus à droite a une valeur constante. Ce calcul se base sur le fait que la dernière colonne à une valeur constante et permet de passer d’une ligne à l’autre. Il faudra attendre le début du XXe siècle pour voir les premières machines à différences commercialisé et suffisamment fiable.

Machines programmables

D’un même temps, des machines « programmables » apparaissent. Tout d’abord dans la musique avec les orgues de barbarie et certaines boites à musique. Dans ce cas, l’instrument produit de la musique via la vibration de lames. Une de ces dernières entrera en vibration par le passage d’un picot sur un cylindre. Chaque lame étant accordée pour produire une note spécifique, la position des picots déterminant ainsi le moment où la note est jouée. Les picots étant sur un cylindre, il « suffit » de changer le cylindre pour changer l’air joué par la boite. Pour les orgues, c’est un peu plus complexe bien que le principe soit similaire. Là ce ne sont pas des picots mais des perforations qui déclenchent le jeu d’une note (par le passage d’air dans un tube). L’utilisation de perforation permet d’utiliser un support plus flexible que pour la boite à musique comme le carton, ce qui simplifie le stockage et le changement de partition/programme.
Ce mécanisme de transfert de l’information part carte perforée a été reprise dans l’industrie du tissage. En effet, l’incrustation de motif dans le tissage est complexe et demande de remonter ou de descendre des fils selon le résultat voulu. Pour faire ce travail au XVIIIe siècle, il faut 2 à 3 personnes autour du métier à tisser et le travail est répétitif et prompt à des erreurs. Basile Bouchon, un ouvrier textile, a le mécanisme des orgues de barbarie au métier à tisser. Ainsi avec un mécanisme, les fils montent et descendent suivant l’information d’un ruban perforé. Son métier permet d’éviter les erreurs de motifs mais nécessite tout de même un·e oppérateur·ice huamin·e qui fait avancer le ruban. Son assistant améliora le métier en utilisant des cartes cartonnées reliées entre elles à la place du ruban. Enfin Joseph Marie Jacquard finit par automatiser le passage des cartes. Son métier à tisser Jacquard ne nécessite alors plus qu’une seule personne pour le manipuler. Outre la réalisation parfaite du motif, l’usage des cartes perforées permet à une même machine de faire tous les motifs possibles en changeant simplement les cartes.

La machine analytique

En travaillant sur les plans de sa machine à différence, Charles Babbage se rend compte qu’il pourrait créer une machine pouvant effectuer des calculs différents, une machine analytique. En effet il sépare deux types d’information qui peuvent être donné à une machine, d’un côté les valeurs numériques et d’un autre côté les opérations à effectuer. Dans sa machine à différences, les opérations sont fixes mais changement de configuration peut modifier celles-ci. Il est donc alors possible de programmer la machine en entrant ces deux types de variables. Il sépare également le lieu où les données sont stockées et où les opérations sont effectuées. Cela permet alors d’appeler deux variables et d’effectuer l’opération demandé. Pour entrer les informations dans la machine, Babbage pense alors aux cartes cartonnés qui fait de même dans le métier Jacquard. Il pense également à une possibilité pour la machine de donner les résultats sous forme de cartes perforées de fait réutilisable pour d’autres calculs. Sa machine a alors tous les éléments d’un ordinateur moderne : une mémoire (le magasin), un processeur (le moulin), une entrée de commande et une sortie du résultat. Néanmoins la machine fonctionne sur un langage en base dix et non en binaire
La séparation des données et des opérations ouvre le champ du possible. En composant une suite d’opérations à partir de plusieurs données de départ et intermédiaire, il est alors possible de réaliser des calculs plus complexes. Babbage et Lovelace présente les différentes étapes de leurs programmes sous forme de tableaux comme-ci-dessous :

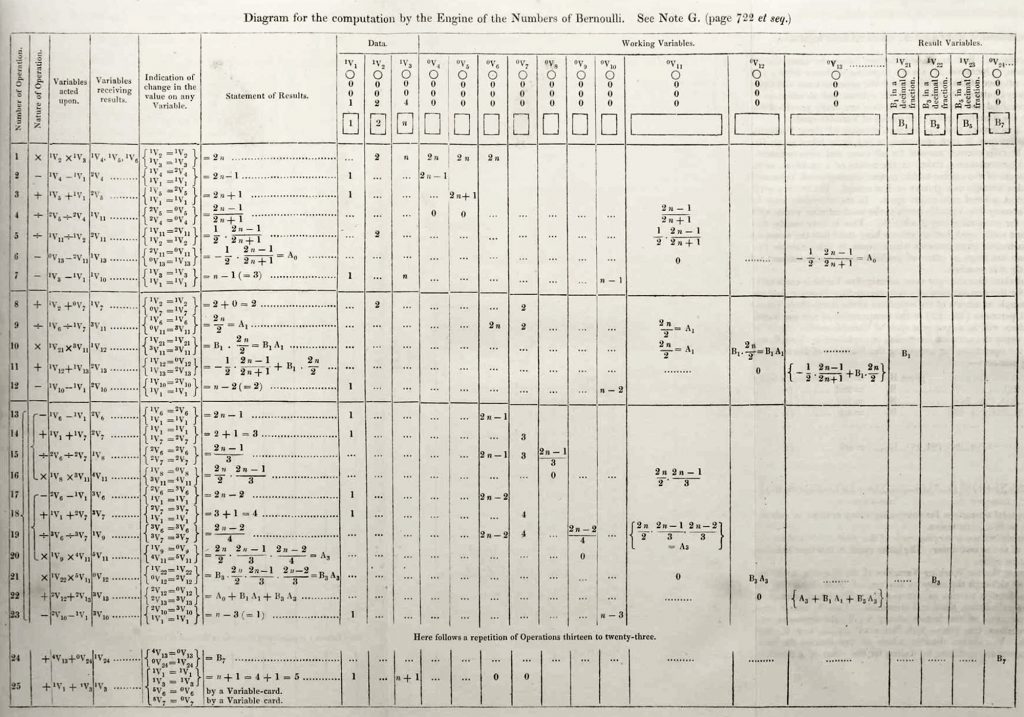
A partir de ce simple principe, il est possible de faire des calculs très complexes. La séparation des données et des opérations permet également de créer des boucles dans le programme. De plus, ce là permet de faire de modifier simplement des variables pour réaliser des calculs appelant des fonctions particulière comme la fonction logarithmique ou cosinus. A partir d’une table écrite sur des cartes perforées transformant une variable calculée par la valeur de celle-ci selon la fonction nécessaire. Cela en fait une machine puissante mais néanmoins pas très rapide.

Si Babbage a l’idée technique de la machine analytique, sans le travail de vulgarisation et l’imagination de Lovelace, la machine aurait pu tomber dans l’oubli. La difficulté de sa construction et l’incapacité de Babbage de s’arrêter sur un plan pour créer un prototype a sonné le glas de la réalisation d’une telle machine. Mais la personnalité et le travail de Lovelace a permis l’idée de perdurer et à ces deux personnes de ne pas être oublier parmi les pionniers de l’informatique même si l’aura de Lovelace fait de l’ombre à Babbage (en même temps, c’est plus souvent l’homme qui éclipse la femme).

Pas tout compris ? Tu as des remarques ? Une erreur s’est glissée dans le texte ? N’hésite pas à laisser un commentaire, j’y répondrais avec plaisir.

Pour aller plus loin :

La série Machines à calculer sur la chaine de Micmath
La traduction de Lovelace de l’article de Ménabréa avec ses notes

Avis et note de Sciences au Cinéma :

La télévision est connue pour ces séries historiques de qualité et la série Victoria est à la hauteur de cette réputation. Si l’image de la souveraine reste relativement lisse, les intrigues des personnages secondaires permettent d’explorer la réalité de l’époque et les questions politiques liées à un monde en changement avec l’industrialisation et l’extension de l’Empire. Néanmoins le faible nombre d’épisode donne lieu à une narration rapide et des sauts dans le temps peu facile à appréhender. De même, si les questions politiques sont développées, les relations –en particulier romantique- entre les personnages prennent une place importante dans le récit et éclipsant, dans l’intérêt du spectateur, les questions politiques. Ces dernières devenant alors de simples éléments de décors au même titre que les costumes.

Victoria, 2016 (en production)
Créée par Daisy Goodwin
Avec Jenna Coleman, Tom Hughes…
Nationalité Britanique (ITV)
Format 60 minutes

Extrait promotionnel de l’épisode 2 saison 2 (en VO) :